
Quantum error correction is a multi-faceted problem. A range of experts are working together to improve the qubits, operating systems and algorithms running on quantum computers to reduce error rates by the orders of magnitude required to solve the range of world-changing problems that quantum computers could crack.
The team I work with are focusing on decoding the vast amounts of data that a quantum computer produces to stop errors propagating and rendering calculations useless. We’re developing a decoder that enables quantum computers to scale to reach their full, vast potential. There are several milestones on this journey, including building a TeraQuop decoder.
But what is a TeraQuop decoder? And why does it matter so much when it comes to cracking quantum error correction?
A TeraQuop decoder would enable a quantum computer to perform a trillion reliable operations – this is important because this represents the scale at which quantum computers start to solve problems that are intractable for any supercomputer. In other words, a TeraQuop decoder helps get us to the point where quantum computers become useful.
Let’s break down each of those terms in TeraQuop decoder to explain how (and why) we’re doing this.
What is a decoder?
Qubits are highly susceptible to noise. This noise could be stray electromagnetic fields, unwanted heating or cooling, cosmic rays, other qubits – anything from the surrounding environment that could cause errors.
There are different types of qubits. An “active” qubit is essentially helping to complete the calculation you’re interested in. If you directly observe an active qubit, this act of observation destroys its quantum state and renders the qubit useless.
That’s why you need large numbers of "syndrome” qubits that you can observe to infer – and then correct – data errors on the active qubits. Together, this cluster of syndrome and active qubits is called one “logical” qubit.
A decoder takes information by measuring many noisy qubits and “decodes” this information to remove the noise. The more qubits used to run a calculation, the more we can reduce errors.
This plot shows the probability of an error occurring reduces to one in a million when we have 161 qubits to create one logical qubit.

But there’s a catch: the more qubits used to make a logical qubit, the slower the decoder becomes. There’s a threshold below which the decoder is not fast enough to correct the errors.
This is where the next term comes in: the Quop.
What is a Quop?
Quop is simply short for a reliable Quantum Operation. In other words, one logical qubit doing one logical (useful) thing.
If we imagine a circuit made up of “N” logical qubits with a depth of logical operations “D”, then the number of Quops “Q” is: Q = N.D
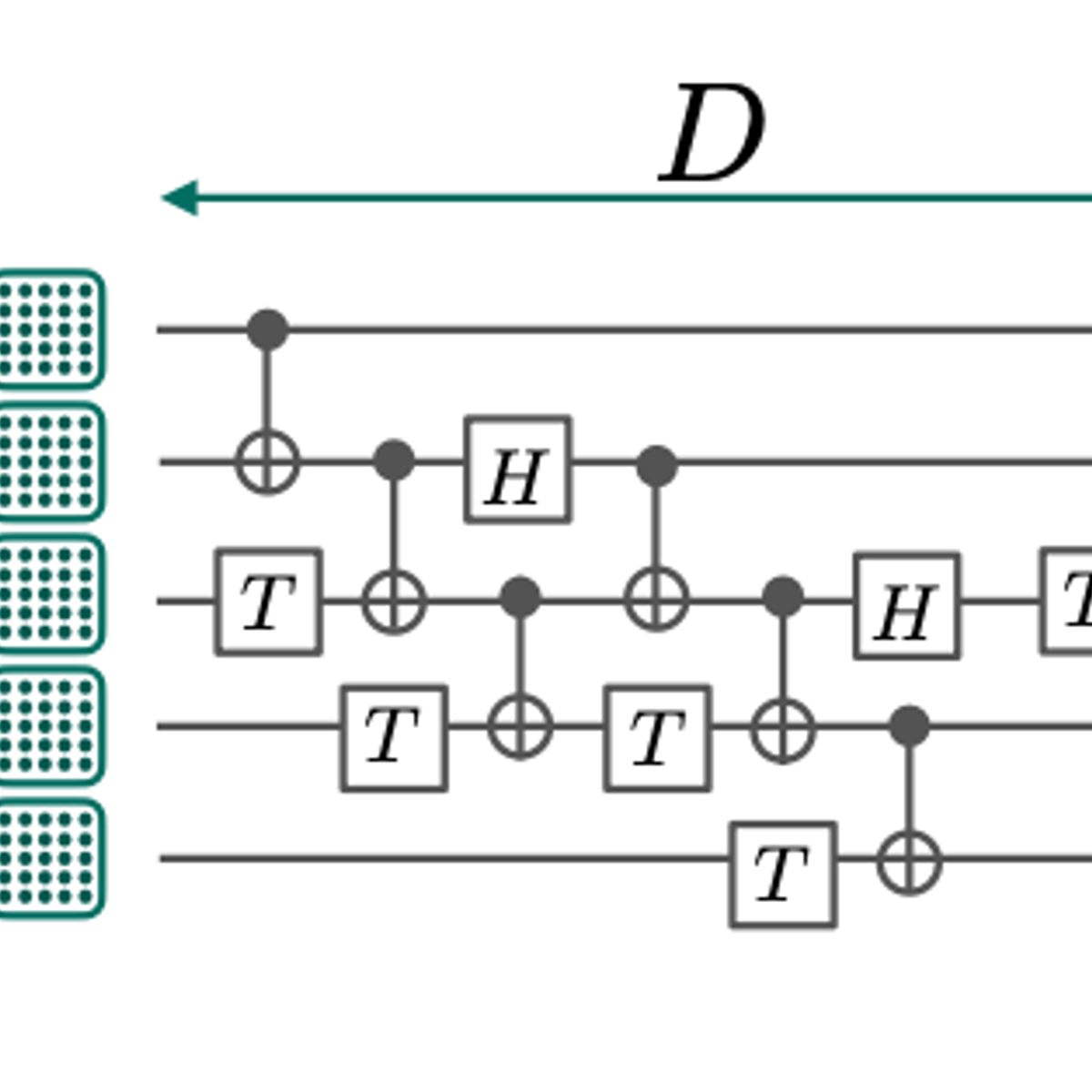
But the reliable part of the Quop definition is also important.
Roughly speaking, we want the error per logical operation “ε” times the number of logical operations “Q” to be less than one: Q.ε < 1.
This is because, otherwise, it is likely that something has gone wrong with our computation.
This error rate ε helps us to understand the reliability of the quantum circuit.
For the decoder to work, we need: N.D = Q ≈ 1/ ε, and we can increase Q further to make the computation even more reliable.
What is a TeraQuop?
Tera simply means a trillion. Similarly, Giga means a billion, Mega means a million and Kilo means a thousand. So, a TeraQuop means a trillion (reliable) quantum operations.
If we plot Q ≈ 1/ ε, we get

We can see that (under some common assumptions about qubit quality) we will need just shy of 1000 qubits to make each logical qubit and reach the Teraquop regime.
This is where the Tera part starts to become important and why we have set ourselves the goal to build a TeraQuop decoder.
Once we have reached the TeraQuop scale then we can start to solve some interesting problems which until now have been out of reach for classical computers.
Remember, Q = N.D where a Quop is a reliable quantum operation (Q), which is the number of logical qubits (N) multiplied by the depth of logical operations (D).
Here are some N and D estimates for some quantum algorithms of interest:

To simulate a free electron gas called jellium, we need approximately 34 GigaQuops. Jellium is a simple example too, a molecule for which classical techniques are pretty good.
When we reach the TeraQuop regime then this is where things start to get interesting and where quantum computers get close to doing something useful for society, for example, by cracking RSA encryption or simulating the FeMoCo molecule.
Looking at these examples, we need 13 TeraQuops (that’s 13 trillion quantum operations) to break RSA encryption.
Simulating FeMoCo could greatly improve the efficiency of converting nitrogen in the air into ammonia, the chemical process which is used in fertilisers. This has implications for addressing food scarcity and global warming. It’s estimated that this process is responsible for 2% of the world's annual energy production, while accounting for 1.4% of global carbon dioxide emissions. We need roughly 285 TeraQuops to simulate FeMoCo.
The FeMoCo example is popular but controversial in scientific circles. However, many different molecules can be simulated with a similar number of Quops, making the milestone notable.
Of course, there are further caveats to these figures:
- The number of Quops could be higher if, for example, we want to increase our confidence in the success of the calculation. This would mean we need to lower the 1 value in the equation Q.ε < 1.
- The number of Quops could also be lower than this TeraQuop target. For example, we’ve assumed that once a fault occurs, then we need to start the calculation again. This might not be the case.
- Quantum algorithms and compilers are also always improving, which could lower the threshold.
So, the TeraQuop threshold could change. But I wouldn’t envisage by much.
Coming back to our original question: what is a TeraQuop decoder? It would be a decoder that is fast enough and accurate enough that we can decode a large enough number of logical qubits to reach a trillion Quops.
A TeraQuop decoder is a solid estimate (give-or-take a few orders of magnitude) to guarantee we have the speed and accuracy to stop errors propagating and rendering calculations useless in large-scale quantum computers.
That’s why we’re building the world’s first scalable quantum error decoder.