Riverlane’s work, entitled ‘Efficient quantum measurement of Pauli operators in the presence of finite sampling error’ has recently been published in the Quantum journal, an open-access peer-reviewed journal for quantum science and related fields.
This paper was a joint effort from many people across the company. Two of the lead authors, Barnaby van Straaten and Daochen Wang, were our summer interns from 2019, highlighting the valuable contributions our interns make. The paper is focussed on maximising the efficiency of a particular part of quantum algorithms such as the variational quantum eigensolver (VQE), a contender for performing computational chemistry calculations on near- or intermediate-term quantum computers.
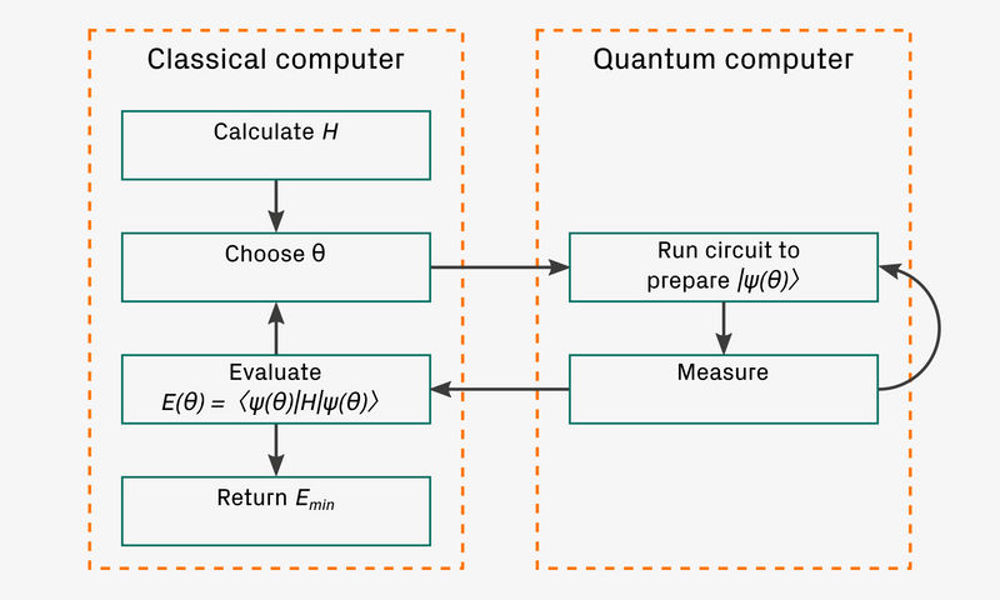
Computational chemistry calculations are thought to be one of the key potential applications of quantum computers. An important quantity of interest in chemical systems is the ground state energy, which corresponds to the lowest eigenvalue of the Hamiltonian operator associated with the system. VQE is an algorithm for finding ground and (with some modification) excited state energies. It is a hybrid algorithm, making use of both classical and quantum computers. In this way, the required quantum computational resources are kept to a minimum. As a result, VQE is potentially thought to be suitable for the noisy intermediate-scale quantum (NISQ) era, when quantum resources will remain limited. An outline of VQE is shown in Figure 1.

Figure 1. An outline of the VQE algorithm, highlighting its hybrid nature. VQE is based on the variational principle, which states that the expectation of an operator on any state is no lower than the smallest eigenvalue of the operator. In VQE, a parameterised set of quantum states, known as an ansatz, is explored to find the state which has the minimum Hamiltonian expectation value. For a given chemical system, the classical computer calculates the Hamiltonian and chooses some values for the parameters, θ. The quantum state corresponding to these parameters is prepared on the quantum computer and measurements made. This is repeated until there are sufficient measurements for the classical computer to construct an estimate of the expectation of the Hamiltonian for the particular state. The classical computer then updates the values of the parameters and this process is repeated until the minimum value of the expectation has been found.
A key part of VQE, as well as many other quantum algorithms, is estimating the expectation value of an operator. Typically, it is not possible to obtain such estimates directly. One simple solution is to decompose the operator into a weighted sum of Pauli operators, which can easily be measured on a quantum computer. Each can then be measured separately, requiring a large number of measurements. An improved method is to collect commuting Paulis together and measure all operators in a particular collection simultaneously. Our paper addresses this approach..
In order to apply such a method, there are two key factors which must be addressed. Firstly, we must understand the improvement offered by a given arrangement of Paulis in collections. In our work, we propose two natural metrics for quantifying this, operating under the assumption that measurements are distributed optimally among collections so as to minimise the overall finite sampling error. Motivated by the mathematical form of these metrics, we introduce Sorted Insertion, a collecting strategy that exploits the weighting of each Pauli operator in the overall sum. Secondly, to measure all Pauli operators with a collection simultaneously, a circuit is required to rotate them to the computational basis. In our paper, we present two efficient circuit constructions which are designed to keep the number of two-qubit gates as small as possible.
Our methods are numerically illustrated in the context of the VQE. As measured by our metrics, Sorted Insertion outperforms four conventional greedy colouring algorithms that seek the minimum number of collections. In Figure 2, we show an estimate of the average reduction in the number of measurements required to obtain an estimate of the expectation of the Hamiltonians of a number of different molecules, relative to measuring each Pauli operator individually. We obtain a speedup factor of about 65 for systems requiring up to 38 qubits.

Figure 2. For different molecular systems, estimates of the average speedup when performing VQE using our SORTED INSERTION method relative to traditional VQE.
View Dr Ophelia Crawford discussing the paper at QCTIP2020